Hello guys and welcome to the 15th tutorial of my OpenGL4 series! Finally I have found time to write this article after almost two weeks! But now I have a bit of free time as it's Easter holiday, and apart from resting and doing nothing I have decided to be at least a bit productive. So I hope you'll enjoy this article! Today, we will discover a new time of shader - geometry shader  .
.
Geometry shader is a brand new type of shader that has a purpose of creating new geometry out of input data. Simple example - you start with rendering points, but actually what you end up with is rendering quads instead. In our case, we will be rendering all points of our mesh and we will end up with rendering of normals instead! Put another way, our input are points and output are lines. So for every single vertex of the mesh, we will generate a new line, that displays its normal! Sounds pretty easy, and actually really is. There are no hidden buts or howevers here, it's as simple as that and all we have to do is to go through the code responsible for that, that should suffice  .
.
First of all, we have to extend our ShaderManager class to support geometry shaders. It's really easy, I will list here all the new things, that have been added:
class ShaderManager
{
public:
// ...
void loadGeometryShader(const std::string& key, const std::string &filePath);
const Shader& getGeometryShader(const std::string& key) const;
private:
// ...
bool containsGeometryShader(const std::string& key) const;
// ...
std::map> _geometryShaderCache;
};
As you can see, I have added a new cache dedicated for geometry shaders and also the trinity of functions to handle geometry shaders - one that loads them (loadGeometryShader), one that gets them (getGeometryShader) and one that checks if such geometry shader exists (containsGeometryShader). You can check their implementations by yourself, but basically it is copy & paste of other shader types with very few changes. The most important one is the type GL_GEOMETRY_SHADER, that we have to put to the loadShader function. With this constant we tell OpenGL, that the shader that's being loaded is a geometry shader  .
.
Now that this has been done, let's proceed with creating a shader program, that displays normals. It consists of three shaders now - vertex shader, geometry shader and fragment shader. Let's go through all of them now.
#version 440 core
layout (location = 0) in vec3 vertexPosition;
layout (location = 2) in vec3 vertexNormal;
out vec3 ioVertexPosition;
out vec3 ioVertexNormal;
void main()
{
ioVertexPosition = vertexPosition;
ioVertexNormal = vertexNormal;
}There is not much to do here. We simply take vertex position and vertex normal and we pass it further to the next stage, which is the geometry shader itself.
#version 440 core
uniform struct
{
mat4 projectionMatrix;
mat4 viewMatrix;
mat4 modelMatrix;
mat3 normalMatrix;
} matrices;
layout(points) in;
layout(line_strip, max_vertices = 2) out;
in vec3 ioVertexPosition[];
in vec3 ioVertexNormal[];
uniform float normalLength;
void main()
{
mat4 pvMatrix = matrices.projectionMatrix * matrices.viewMatrix;
vec4 firstNormalPoint = matrices.modelMatrix*vec4(ioVertexPosition[0], 1.0);
gl_Position = pvMatrix * firstNormalPoint;
EmitVertex();
vec3 transformedNormal = normalize(matrices.normalMatrix*ioVertexNormal[0]);
vec3 normalWithLength = transformedNormal * normalLength;
vec4 secondNormalPoint = firstNormalPoint + vec4(normalWithLength, 0.0);
gl_Position = pvMatrix * secondNormalPoint;
EmitVertex();
EndPrimitive();
}
Now this is where it gets interesting. First of all, we have moved matrices uniform to this stage, because here we will actually be doing all transformations instead. But that's not as significant as next lines of code. The lines starting with the layout keyword are the important ones. The first layout(points) in line is to tell OpenGL, what is our input. This time the input are single points, no lines, no triangles, just points. The second layout(line_strip, max_vertices = 2) out line is telling OpenGL, what is our output type - in our case it's a line strip. So out of a point we create a line (strip)  .
.
You might ask yourself now - why line strip and why not simply a line(s)? The reason for that is, that there are actually 3 supported output geometry types there - points, line_strip and triangle_strip. The thing is, that using line_strip we can render lines as well, so that is no problem  . Same would apply for triangles and triangle_strip (check Khronos Wiki for Geometry Shaders). They work just as you would expect with their OpenGL counterparts. In the layout line, there is also max_vertices defined. This is a must have thing and it's a constant to tell OpenGL, how many vertices are you planning to output at most (probably driver can do some inner optimizations then). In our case, we get a point and we output a line, so that makes it 2 vertices. There is a limitation to it - this number can't be larger than the implementation-defined limit, which one can query using glGetInteger function and using GL_MAX_GEOMETRY_OUTPUT_VERTICES constant
. Same would apply for triangles and triangle_strip (check Khronos Wiki for Geometry Shaders). They work just as you would expect with their OpenGL counterparts. In the layout line, there is also max_vertices defined. This is a must have thing and it's a constant to tell OpenGL, how many vertices are you planning to output at most (probably driver can do some inner optimizations then). In our case, we get a point and we output a line, so that makes it 2 vertices. There is a limitation to it - this number can't be larger than the implementation-defined limit, which one can query using glGetInteger function and using GL_MAX_GEOMETRY_OUTPUT_VERTICES constant  .
.
Now we proceed with two input variables - ioVertexPosition and ioVertexNormal - and a uniform variable normalLength. Those two are input variables from the previous stage. You might ask yourself why is it an array now. The answer is simple - our input geometry might not be only points, but also lines, triangles etc. Those don't have just one vertex, but generally N vertices. But since we have points as input, those arrays will actually have length 1. Uniform normalLength simply defines the length of rendered normal (which you can by the way control to see the effect  ).
).
And now come the most important part - how to calculate both points correctly. First of all, we calculate pvMatrix, which is projection multiplied by view matrix. We will need that by both points of normal, that's why it's stored in a variable. Let's calculate first normal point. This one is easy, we just take the input point and multiply it by model matrix. This way, we will get the world position of this vertex and all we have to do now is to use our pvMatrix and multiply our already transformed point with it. As it was previously with vertex shader, we have to set the built-in variable gl_Position.
What is really important is the line after, that says EmitVertex(). This is a built-in geometry shader function, that actually creates one vertex of our generated primitive. By calling it, we are like confirming the first point of our normal line. Now we have to do the same with the second point. To calculate second point of the line, we have to take our mormal and transform it using normal matrix to obtain transformed normal (stored in a variable transformedNormal). After normalizing it, we can now change its length with our uniform normalLength. Having first point and a transformed normal, calculating second point is simply a matter of adding together first line point and a transformed normal  .
.
When second point has been calculated and emitted, there is yet another important function to call and it's EndPrimitive(). The thing is, that with geometry shader you can possibly emit multiple primitives as well! But now that we have emitted two vertices, that represent our normal and we're actually done this time, we have to confirm this by calling the EndPrimitive() method. Otherwise, we would not see anything!
#version 440 core
out vec4 outputColor;
void main()
{
outputColor = vec4(1.0, 1.0, 1.0, 1.0);
}
After this thorough and long explanation of the geometry shader, luckily there is not much to tell about the fragment shader. All we do is output a pure white color to render normals with  .
.
To utilize our new code and knowledge, we have to create a shader program, that displays normals. We do this in the initializeScene function:
void OpenGLWindow::initializeScene()
{
try
{
// ...
sm.loadVertexShader("normals", "data/shaders/normals/normals.vert");
sm.loadGeometryShader("normals", "data/shaders/normals/normals.geom");
sm.loadFragmentShader("normals", "data/shaders/normals/normals.frag");
// ...
}
catch (const std::runtime_error& ex)
{
// ...
}
// ...
}
To render normals of our geometry, we have to render it in two passes - first pass is a normal render just as we are used to and in the second pass, we have to render the geometry using normals shader program and as points instead of triangles. For this reason, I had to add a new function to the StaticMesh3D class called renderPoints, which doesn't render the given primitive normally, but rather as points instead (check the implementation for each primitive, it's really simple  ). The final code snippet renders normals of our geometry:
). The final code snippet renders normals of our geometry:
void OpenGLWindow::renderScene()
{
// ...
if (displayNormals)
{
// Set up some common properties in the normals shader program
auto& normalsShaderProgram = spm.getShaderProgram("normals");
normalsShaderProgram.useProgram();
normalsShaderProgram[ShaderConstants::projectionMatrix()] = getProjectionMatrix();
normalsShaderProgram[ShaderConstants::viewMatrix()] = camera.getViewMatrix();
normalsShaderProgram[ShaderConstants::normalLength()] = normalLength;
// Render all the crates points
auto matrixIt = crateModelMatrices.cbegin();
for (const auto& position : cratePositions)
{
normalsShaderProgram.setModelAndNormalMatrix(*matrixIt++);
cube->renderPoints();
}
// Proceed with rendering pyramids points
matrixIt = pyramidModelMatrices.cbegin();
for (const auto& position : pyramidPositions)
{
normalsShaderProgram.setModelAndNormalMatrix(*matrixIt++);
pyramid->renderPoints();
}
// Finally render tori points
matrixIt = torusModelMatrices.cbegin();
for (const auto& position : toriPositions)
{
normalsShaderProgram.setModelAndNormalMatrix(*matrixIt++);
torus->renderPoints();
}
}
}
This code is pretty straightforward, one thing that might be confusing a bit is this matrixIt. What is this? I am not fan of copy & pasting code, so in this first pass, where we render our geometry normally, I am storing model matrices of our geometry to the correspoding vectors, just to re-use it when rendering normals. The thing is, that the rendered objects have different positions / rotations / sizes and in order to prevent copy & paste, I have to cache the matrices and re-use them later. That's the whole point of this matrix iterator - I go through the cached values and apply the matrices in the same order as I did before  .
.
And that was it, that's everything I had to explain! The result is really good IMHO:
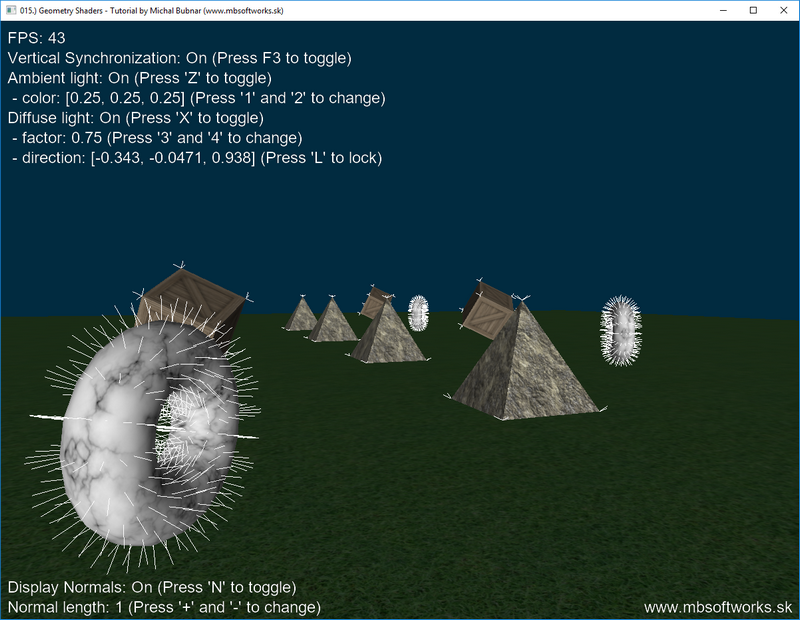
Today, we have learned a brand new shader type and we have also learned, how to utilize it in order to render geometry normals. There are however many other usages of the geometry shaders, that I will cover, but not in this tutorial. One thing that I don't like about this tutorial is, that it doesn't contain many images, but only much text  . If you've made it up to here despite the lack of pictures, I thank you for reading through it! Stay tuned for another wisdom that I bring next and enjoy the Easter Holidays 2019
. If you've made it up to here despite the lack of pictures, I thank you for reading through it! Stay tuned for another wisdom that I bring next and enjoy the Easter Holidays 2019  .
.
 Download 3.35 MB (1007 downloads)
Download 3.35 MB (1007 downloads)