Welcome to the 4th tutorial of my OpenGL4 tutorial series! In this one, we're getting real serious here, as we will not only have our first 3D scene, but we will also begin with the most simple animation, how to correctly calculate frame rate and animate our scene depending on the time passed! Let's dive into it right away!

First of all, we have to clarify some really important and pretty common terms, when it comes to 3D graphics. You might have heard, but there are several coordinate spaces and you should definitely know what is what. In this tutorial, we are going to focus on four important spaces - Model Space, World Space, Camera (View) Space and Screen Space.

This is the coordinate system local to the object, therefore sometimes it's referred to as object space as well. Let's take the cube from this tutorial as an example - the cube itself is a 3D model, and we need basically 8 vertices to represent it. Let's have a look at the cube and its coordinates.

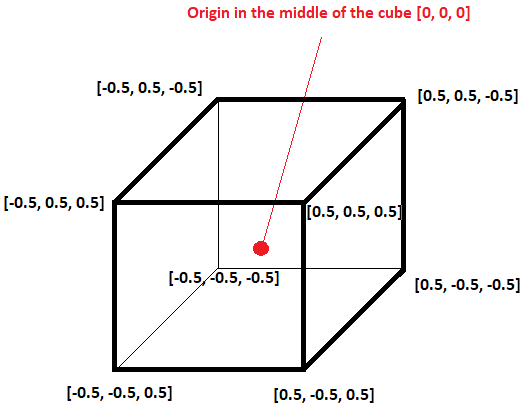
As you can notice, the origin is in the center of the cube and all its vertices revolve around it. I have also chosen the 0.5 size in every direction, so that the cube has a unit size in every direction. This way, the cube will be easily scaled / shrunk uniformly in all directions!

Now that our cube is somewhere defined, we don't want it to actually remain at position [0, 0, 0] forever. Let's say, that we want to render the cube in a way, that it's center is at position [25, 0, 0]. So if we translate the cube's position by this vector, we will get the cube's coordinates again, but this time in world space! That means, the actual position of the coordinates in the world! Look at the picture:

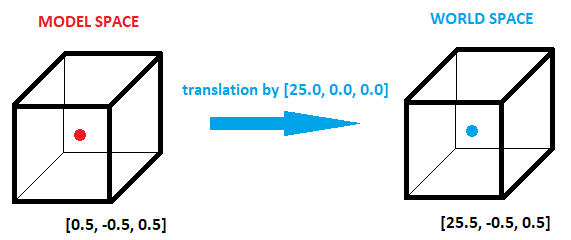
You can see that with origin of the cube moved, all its vertices have moved too! In the picture, you might see, that the point [0.5, -0.5, 0.5] in the model coordinates has become [25.5, -0.5, 0.5] in the world coordinates. The same principle holds true for other transformations, like rotation, or scale - model vertices they do not change, but they are rather transformed into the world space .

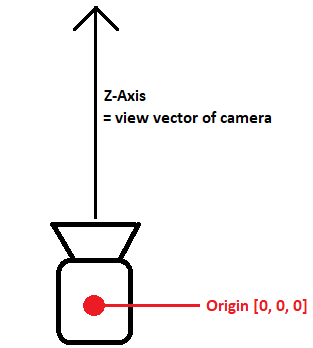
When we have world space coordinates, now we need to transform them to camera space, sometimes also referred as view space. The easiest way to think of programming 3D graphics is to imagine, that we have a camera and that camera has some position and it looks in particular direction. And that is what camera space is about. The origin point is actually camera's position and Z-axis is the direction the camera looks to. Then we align whole scene in such way, that all the points remain same, but transformed relative to the camera! Just look at the picture below:

The last space we need to discover is screen space. This time, it's not 3D, but 2D and usually represents the X,Y coordinate system of the screen you are rendering too (usually in pixels). That is what the user finally sees.

To get from one space to another, one uses matrix to do so. Matrix encodes the whole transformation and all we have to do is to multiply the matrix with input vertex / vector to get there . The following list should help you to understand, what matrices you need to get from one space to another:

• Model Space => World Space: model matrix - for every object in scene, this matrix is usually different (because different objects have different positions, rotations etc.)
• World Space => Camera Space: view matrix - this matrix is usually calculated only once per frame and is can be re-used, until the camera position or view direction changes (then it must be recalculated)
• Camera Space => Screen Space: projection matrix - this matrix is usually calculated only when you change the size of a window and you have different widths / heights

Fortunately, matrices and all kinds of utility functions for working with them are implemented already! The glm library supports calculating all of the matrices mentioned above and we will cover this now. The matrices are also supported by GLSL natively and we can directly use them in shader programs !

Model matrix is probably the easiest one. There are 3 main operations that you can perform - translate, rotate and scale. Translation moves our object around the scene, with rotation and scale we can rotate and enlarge / shrink our objects. To calculate the operations mentioned, we need following glm functions:

• glm::translate - translates the given matrix by the given glm::vec3
• glm::rotate - rotates the given matrix by the given angle (in radians) on given glm::vec3 axis
• glm::scale - scales the given matrix by the given glm::vec3 vector (in X, Y and Z direction)

The order we combine these transformations is really important here! The translate / rotate / scale order is usually the correct one. If, for instance, you performed rotation by 90 degrees on Y axis and afterwards translated by 10 units on X axis ([10, 0, 0]), you would be actually moving along Z axis, because you have rotated before! So as a general rule, first move (translate) to the desired location, then rotate and scale at the end .

As an example, let's take the pyramid in the top-left corner, how exactly is it transformed:

glm::mat4 modelMatrixPyramid = glm::mat4(1.0); // We start with identity matrix
modelMatrixPyramid = glm::translate(modelMatrixPyramid, glm::vec3(-12.0f, 7.0f, 0.0f)); // Translate first
modelMatrixPyramid = glm::rotate(modelMatrixPyramid, currentAngle, glm::vec3(0.0f, 1.0f, 0.0f)); // Then rotate
modelMatrixPyramid = glm::scale(modelMatrixPyramid, glm::vec3(3.0f, 3.0f, 3.0f)); // Scale at last

Just to get the good grasp of it, try exchanging the order of those operations as homework, and see by yourself, what happens . You can also combine multiple translations or rotations.

Now, that we've got from model space to the world space, it is time to get further to the view space. This means, that we have to calculate view matrix. Fortunately, there is a function in glm library to calculate this for us again! Explaining the logic behind this function is beyond the scope of this humble article, so just know, that it is already implemented and that it works . I will maybe one day start a separate article series about matrices and 3D math in general, there is so much there to explain and understand .

Anyway, I got carried away a bit, let's get back to the topic. This is the code you can calculate the view matrix using glm library with:

glm::mat4 viewMatrix = glm::lookAt(glm::vec3(0.0f, 0.0f, 20.0f), // Eye position
glm::vec3(0.0f, 0.0f, 0.0f),  // Viewpoint position
glm::vec3(0.0f, 1.0f, 0.0f)); // Up vector

This function requires three arguments - eye position, viewpoint position and up vector. Let's examine them:

• Eye position: super simple, it's simply where eye, or camera is located, in another words - camera's position
• Viewpoint position: it's the point, to which camera is directed, or looks upon. Put simply - eye looks at that point, so it defines where we look at
• Up vector: notice, that this is not a position anymore, but vector (direction) instead. Usually, you set this to (0, 1, 0). What does it mean? Imagine, that you're looking normally with your head, straight. That's when up vector is (0, 1, 0), because the direction to "up" is simply on Y axis, vertical, to the top. But if you tilt your head by 90 degrees, while still looking the same direction, your up vector changes to let's say (1, 0, 0). But you see the world rotated now!

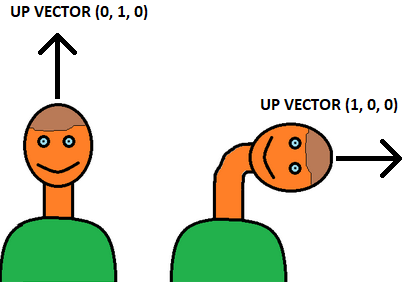
I really hope, that this simple, yet powerful illustration has helped you to understand the point . In a dynamic scene, where you (the camera) moves around, this view matrix has to be calculated every frame (because position and viewpoint change). But in case of our tutorial, where camera is simply static and never moves, we can calculate this matrix only once (that's why we are doing this in initializeScene() method only).

Now that we could get to the camera (view) space, we can start projecting 3D scene onto 2D screen and we need to calculate the projection matrix. As usual, glm library gives us a helping hand and we can directly calculate it simply by calling the following function:

glm::mat4 projectionMatrix = glm::perspective(
    45.0f, // field of view angle (in degrees)
    float(width) / float(height), // aspect ratio
    0.5f, // near plane distance
    1000.0f); // far plane distance

As before, let's go through the parameters.

• Field of view angle: defines, how much can we actually see, or the angle, the camera's view stretches to
• Aspect ratio: the ratio between width and height of the screen we are projecting to (our window's width and height usually)
• Near plane distance: what distance is the closest, that we can see actually (anything closer to the camera than this will simply disappear)
• Far plane distance: what distance is the furthest, that we can see (and what is the furthest that will be projected, anything beyond disappears too)

As you can see, the only thing that is changing here is usually the window size and height. That is why, the recalculation of projection matrix takes place only, when we change the size of a window and at the startup. Otherwise, we really don't have to change the perspective matrix, unless we really do some funky stuff. You can have a look at the code of OpenGLWindow class - anytime the window's size changes, we do the recalculation.

Now that we know what to do, let's look at the important parts of the code, that are operating with matrices.

The most of magic happens in the vertex shader, so let's examine it:

#version 440 core

uniform struct
{
	mat4 projectionMatrix;
	mat4 viewMatrix;
	mat4 modelMatrix;
} matrices;

layout(location = 0) in vec3 vertexPosition;
layout(location = 1) in vec3 vertexColor;

smooth out vec3 ioVertexColor;

void main()
{
	mat4 mvpMatrix = matrices.projectionMatrix * matrices.viewMatrix * matrices.modelMatrix;
	gl_Position = mvpMatrix * vec4(vertexPosition, 1.0);
	ioVertexColor = vertexColor;
}

You should be already familiar with things like in/out variables and location. But there, we see something brand new. It's that uniform struct thingy. This whole construct there is a uniform variable, which is another important concept in the shaders world. Uniform variables are something, that you can set from your program (from client side), and you can set them before you issue rendering commands. During rendering, uniform variable values cannot be changed (that's why it is called uniform actually).

In our case, we have matrices to set - model, view and projection, just as described above. To keep everything nice and systematic, we have all matrices in a struct called matrices (so that if we want to access it, we can do it using matrices.something, just like you do in C or C++ structs). Later, we use these matrices in the main method of the vertex shader. We can actually combine all three matrices to create so called MVP matrix (modelview-projection matrix). If we multiply this matrix with our incoming vertices, we can set the result directly to the gl_Position variable!

We also have to care about the order - the correct order of multiplication is projectionMatrix * viewMatrix * modelMatrix. With this final matrix, we can then multiply the matrix with the vertex position. You may have noticed, that this vertex position is vec3, but I have extended it to vec4 by adding that 1.0 to the end as w coordinate. What is this? Well, to be able to multiply the 4x4 matrix with vertex, vertex also has to have 4 components. This fourth component is to make vertex position in Homogeneous coordinates. Again, explaining this is beyond scope of article (maybe one day, where there will be 3D math series, I will link to my own article, but the linked article does pretty good job in explaining this). Simply said, to get the real X, Y, Z position of the vertex in homogeneous coordinates, you need to divide all three components by that W component . After extending our vertex, the multiplication is possible (4x4 matrix with 4x1 vertex).

The rest (setting output color of the vertex) is the same as it was in previous tutorial.

The fragment shader has not changed at all since previous tutorial. Once we get interpolated fragment color, we just output it, nothing else .

Below, you can see the rendering code, the renderScene function of this tutorial. Not everything is copied here, but you will get the point:

void OpenGLWindow::renderScene()
{
	glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

	mainProgram.useProgram();
	glBindVertexArray(mainVAO);

	mainProgram["matrices.projectionMatrix"] = getProjectionMatrix();
	mainProgram["matrices.viewMatrix"] = viewMatrix;

	// Render rotating cube in the middle
	auto modelMatrixCube = glm::mat4(1.0);
	modelMatrixCube = glm::rotate(modelMatrixCube, currentAngle, glm::vec3(1.0f, 0.0f, 0.0f));
	modelMatrixCube = glm::rotate(modelMatrixCube, currentAngle, glm::vec3(0.0f, 1.0f, 0.0f));
	modelMatrixCube = glm::rotate(modelMatrixCube, currentAngle, glm::vec3(0.0f, 0.0f, 1.0f));
	modelMatrixCube = glm::scale(modelMatrixCube, glm::vec3(5.0f, 5.0f, 5.0f));
	
	mainProgram["matrices.modelMatrix"] = modelMatrixCube;
	glDrawArrays(GL_TRIANGLES, 0, 36);

	// Render 4 pyramids around the cube...

	currentAngle += glm::radians(sof(90.0f));

    // ..
}

You can see, that in the lines above, we are calculating the model matrix of the cube by rotating it with a specific angle (currentAngle, in radians) and then scaling the cube by the factor of 5. At the end of rendering, we increase that angle by 90 degrees per second (this is achieved by strange-sounding function sof explained a bit further in the article). You can also see those peculiar lines of code there, like this one:

mainProgram["matrices.projectionMatrix"] = getProjectionMatrix();

Here we actually set the value of the uniform variable in the shader. I won't get much into implementation details, it makes use of C++ operator overloading, but long story short - to set uniform variable, one needs to get the uniform location (every uniform has its location assigned by OpenGL). This is done by calling the function glGetUniformLocation(shaderProgramID, "uniform_variable_name") Afterwards, you can call a family of glUniform functions to set integers, floats, doubles, vertices, matrices etc. Check files uniform.h and uniform.cpp for the real implementation details.

When uniforms have been set, we can call classic glDrawArrays function to perform actual rendering .

There is one last aspect that I have implemented in this tutorial, and it's counting Frames Per Second, or simply FPS. This is also implemented in the OpenGLWindow class, the function is called updateDeltaTimeAndFPS():

void OpenGLWindow::updateDeltaTimeAndFPS()
{
	const auto currentTime = glfwGetTime();
	_timeDelta = currentTime - _lastFrameTime;
	_lastFrameTime = currentTime;
	_nextFPS++;

	if(currentTime - _lastFrameTimeFPS > 1.0)
	{
		_lastFrameTimeFPS = currentTime;
		_FPS = _nextFPS;
		_nextFPS = 0;
	}
}

In this function, we're making use of glfwGetTime() function. It returns number of elapsed seconds, since GLFW has been initialized. How to use it to calculate FPS? It's pretty simple - we have to keep track of the last time, that we have updated FPS count and every frame, request the new time. If the new time minus last time of update is more than one second, we need to update FPS. In the variable _nextFPS, we keep track of the next actual value of FPS and whenever one second elapses, real FPS is set to its value and then it's reset to 0. In other words, we are counting, how many FPS have there been during last second and then we update it. Pretty simple! To retrieve this value, there is another function called getFPS(). It's also called in the renderScene function and I am setting the window title with current FPS value .

In this function, there is also _timeDelta value calculated. This stores, how many seconds have elapsed since the last frame render. Why do we need this? Say that we want to increase some value by 100.0 per second, then you need to multiply one hundred with this delta. Let's say, that 100 ms (0.1 seconds) have elapsed since the last frame (that means you have probably slow computer and you will get around 10 FPS). That means, we have to move by 100.0 * 0.1 = 10.0 units to keep the pace of 100.0 units per second! This all is implemented in the function called sof . This strange name stands for Speed Optimized Float - it takes the input value and multiplies it with that time delta. Backstory to this - I've been using this name in my very first OpenGL programming projects, so I wanted to keep the legacy .

After so much work, the result is definitely worth it:

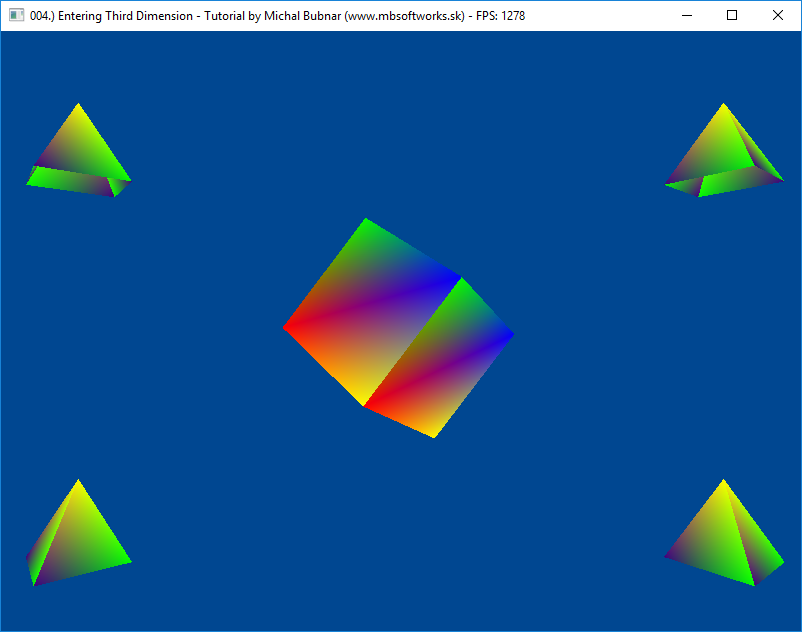
There is really much knowledge behind 3D graphics and it's not that easy to explain all those concepts in one simple article. I guess you don't really how to know everything to the greatest detail as long as you understand the principles and can live with it. With enough experience, you will eventually understand the subtle details in 3D graphics and all the knowledge will start making perfect sense. So take your time, let it rest in your head and prepare for the next tutorial, that will come soon .