Hello fellow people of the internet! This is my 6th tutorial in the OpenGL4 series and in this one, we will upgrade our boring walking camera to a flying one, where you can freely move around the world and even reach the skies ! It's going to be the same camera style as you know from FPS (first person shooter) computer games. Wanna learn, how to do it? Then keep reading!

First of all, let's have a look at the flying camera class itself. It's basically very similar to the camera class from the previous tutorial, but it has some new functions and features:

class FlyingCamera
{
public:
	FlyingCamera(const glm::vec3& position, const glm::vec3& viewPoint, const glm::vec3& upVector, float moveSpeed = 10.0f, float mouseSensitivity = 0.15f);

	void setMoveSpeed(float moveSpeed);
	void setMouseSensitivity(float mouseSensitivity);
	void setControls(int forwardKeyCode, int backwardKeyCode, int strafeLeftKeyCode, int strafeRightKeyCode);
	void setWindowCenterPosition(glm::i32vec2 windowCenterPosition);

	glm::mat4 getViewMatrix() const;

	void update(const std::function& keyInputFunc,
		const std::function& getCursorPosFunc,
		const std::function& setCursorPosFunc,
		const std::function& speedCorrectionFunc);

private:
	void moveBy(float distance);
	void strafeBy(float distance);
	void rotateLeftRight(float angleInDegrees);
	void rotateUpDown(float angleInDegrees);

	glm::vec3 getNormalizedViewVector() const;

	glm::vec3 _position;
	glm::vec3 _viewPoint;
	glm::vec3 _upVector;

	glm::i32vec2 _windowCenterPosition;
	float _mouseSensitivity;

	float _moveSpeed;
	int _forwardKeyCode;
	int _backwardKeyCode;
	int _strafeLeftKeyCode;
	int _strafeRightKeyCode;
};

I guess the easiest way to explain this is to list all the new functions with a brief explanation first and then go through them in more detail:

• void setMouseSensitivity(float mouseSensitivity)
  This here defines, how much shall we rotate the camera when we move with the mouse. That sensitivity parameter means, by how many degrees should the view rotate, when you move mouse by 1px
• void setWindowCenterPosition(const glm::i32vec2& windowCenterPosition)
  Using this method you tell the camera class, where is the center point of your OpenGL window in the screen units (we will need that later, you will learn why)
• void strafeBy(float distance)
  Strafing is the new concept used by this camera, it's when you go to the left and right with the camera without changing your view direction (sidestepping)
• void rotateLeftRight(float angleInDegrees)
  This is a helper function, that cares about rotating view just to the left and to the right. This one is quite simple and is basically same as in previous tutorial
• void rotateUpDown(float angleInDegrees)
  Another helper function, that cares about rotating the camera view up and down. There is more to it than you might think, so it deserves further explanation

If we want to control camera with mouse, the standard way (or at least the one I know of and have seen so far) is to simply reset cursor position everytime to the same pre-defined point every single frame (in our case it's center of the window) and when mouse movement occurs, we calculate the difference between that point and current cursor position and then we reset the cursor position back. If we haven't reset cursor's position, eventually during rotating we would have reached the edge of the screen and we could not rotate anymore (you can't go with mouse cursor beyond screen), so that's the reason why we do it like that .

Let's analyze the update() function, which is performing the rotation with the mouse:

void FlyingCamera::update(std::function keyInputFunc,
	std::function getCursorPosFunc,
	std::function setCursorPosFunc,
	std::function speedCorrectionFunc)
{
	// ... key input ...

	auto curMousePosition = getCursorPosFunc();
	auto delta = _windowCenterPosition - curMousePosition;

	if (delta.x != 0) {
		rotateLeftRight(float(delta.x) * _mouseSensitivity);
	}

	if (delta.y != 0) {
		rotateUpDown(float(delta.y) * _mouseSensitivity);
	}

	setCursorPosFunc(_windowCenterPosition);
}

As you can see, update function takes as parameter two new functions - one for getting current cursor position and one for setting current cursor position. First we get the current position by calling getCursorPosFunc() and afterwards we calculate delta - the offset by how many pixels have you moved the cursor with the mouse since last frame. If the user has moved mouse left or right, that means, that delta.x is not 0 and we can rotate the view to left or right by calling rotateLeftRight(angle). Angle (in degrees) is calculated as float(delta.x) * _mouseSensitivity. That means, for every pixel we have moved, we rotate the view by mouseSensitivity, which is by default set to 0.15f. rotateLeftRight method is implemented same way as it was in the previous tutorial, there is really no difference - we just rotate around Y-axis

Same goes for the delta.y. If there is non-zero delta.y, we can rotate the view up or down by calling rotateUpDown(angle) method. Angle is calculated the same way as by rotating left-right. There is however some trickery here. Unlike rotating left-right, where we simply rotate around the same axis everytime, in case of up and down, we have to calculate the axis that we rotate around. Just look at the picture below:

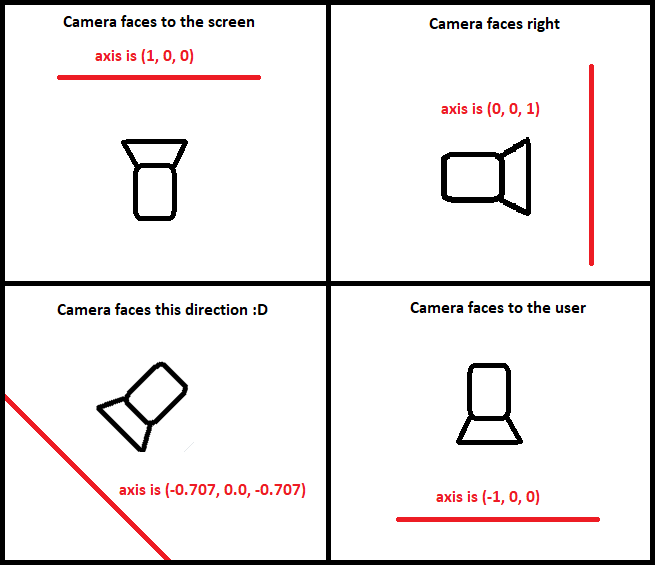
The thing is - depending on the angle camera is facing, we have to calculate the axis, that we will rotate the view up and down around. This is the only tricky part here. Luckily, this actually isn't as hard as it seems - all we have to do is to calculate cross product of two vectors. One of them is really easy, it's up vector of the camera and the second is the view direction. Calculating cross product of those two vectors and normalizing it will give us the required axis to rotate around!

There is one small thing we have to care about when implementing up and down rotation. Unlike left-right rotation, we cannot rotate indefinitely up and down - you can't tilt your head 360 degrees up and down . That's why I have implemented a cap for rotating the camera up and down to 85 degrees up and 85 degrees down. In order to do that, we have to calculate the angle of rotation up and down and then make sure, that by rotating our camera we don't exceed our rotation cap 85 degrees. We would like our angle to correspond to this picture:

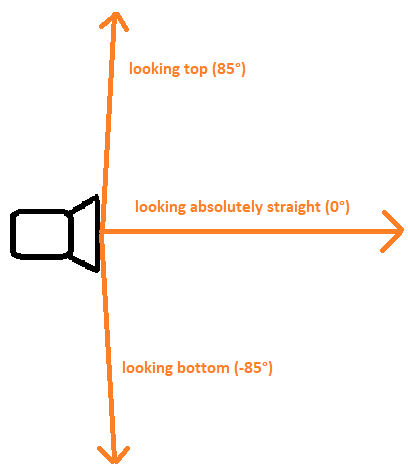
Calculating this angle is pretty easy. Let's have a look at the code first and then explanation:

void FlyingCamera::rotateUpDown(float angleInDegrees)
{
	glm::vec3 viewVector = getNormalizedViewVector();
	glm::vec3 viewVectorNoY = glm::normalize(glm::vec3(viewVector.x, 0.0f, viewVector.z));

	float currentAngleDegrees = glm::degrees(acos(glm::dot(viewVectorNoY, viewVector)));
	if (viewVector.y < 0.0f) {
		currentAngleDegrees = -currentAngleDegrees;
	}

	// ... rotation (later)
}

We are just taking the view vector and we create another vector called viewVectorNoY by neglecting y component completely, thus obtaining same direction we're facing, but denying up and down camera tilt completely. When we calculate the angle between those two vectors (using acos method, for more information, refer to the Angle between vectors article), we have to make sure, that the new angle - angle after rotation does not exceed our limits. If it does not, we can perform the rotation itself! Notice that if (viewVector.y < 0.0f) condition - the angle calculated cannot be negative, but we know that it's negative, when we're looking down - we can simply check, if y component of our view vector is below 0.0 and we negate the angle. Let's examine the code of rotation then:

void FlyingCamera::rotateUpDown(float angleInDegrees)
{
	// ... calculating camera angle

	if (newAngleDegrees > -85.0f && newAngleDegrees < 85.0f)
	{
		glm::vec3 rotationAxis = glm::cross(getNormalizedViewVector(), _upVector);
		rotationAxis = glm::normalize(rotationAxis);

		glm::mat4 rotationMatrix = glm::rotate(glm::mat4(1.0f), glm::radians(angleInDegrees), rotationAxis);
		glm::vec4 rotatedViewVector = rotationMatrix * glm::vec4(getNormalizedViewVector(), 0.0f);

		_viewPoint = _position + glm::vec3(rotatedViewVector);
	}
}

It's basically the same as it was by left-right rotation, however now we have to calculate the axis of rotation, as mentioned above, using cross product. After getting rotation matrix, we multiply it with view vector to obtain rotate view vector and that's it! Hope that my explanation makes sense, this stuff isn't exactly the easiest to understand.

When we already have rotation with mouse, we can re-use left and right arrow to perform strafing instead of rotating. In other words, it's sidestepping. This one is pretty easy - we just have to calculate vector of strafing we have to move along. Just look at the code itself first:

void FlyingCamera::strafeBy(float distance)
{
	glm::vec3 strafeVector = glm::normalize(glm::cross(getNormalizedViewVector(), _upVector));
	strafeVector = glm::normalize(strafeVector);
	strafeVector *= distance;

	_position += strafeVector;
	_viewPoint += strafeVector;
}

Strafe vector is just cross product between the view direction and the up vector! We also should make sure, that the y component is 0.0, so that we don't move along y-axis during strafe. But this is already achieved! That's because our up vector is (0, 1, 0) and this will ensure, that the y component of the cross product will be zero! Because result of cross product is not normalized in general, we have to normalize it too. Afterwards, it's just a matter of moving camera's position and view point along that axis by specified distance . Let's see the update function and how we use keys to move:

void FlyingCamera::update(std::function keyInputFunc,
	std::function getCursorPosFunc,
	std::function setCursorPosFunc,
	std::function speedCorrectionFunc)
{
	if (keyInputFunc(_forwardKeyCode)) {
		moveBy(speedCorrectionFunc(_moveSpeed));
	}

	if (keyInputFunc(_backwardKeyCode)) {
		moveBy(-speedCorrectionFunc(_moveSpeed));
	}

	if (keyInputFunc(_strafeLeftKeyCode)) {
		strafeBy(-speedCorrectionFunc(_moveSpeed));
	}

	if (keyInputFunc(_strafeRightKeyCode)) {
		strafeBy(speedCorrectionFunc(_moveSpeed));
	}

	// ... rotation with mouse
}

Strafing is simply now a matter of calling the strafeBy function and providing either positive value to go right or negative to go left .

What changes from the previous tutorial is just correct way of calling the update() function of the camera. Now, we need to provide not only key input and speed correction function, but also two additional functions - one for getting mouse cursor position and one for setting mouse cursor position :

void OpenGLWindow::handleInput()
{
	// ... other keys handling

	int posX, posY, width, height;
	glfwGetWindowPos(getWindow(), &posX, &posY);
	glfwGetWindowSize(getWindow(), &width, &height);
	camera.setWindowCenterPosition(glm::i32vec2(posX + width / 2, posY + height / 2));

	camera.update([this](int keyCode) {return this->keyPressed(keyCode); },
		[this]() {double curPosX, curPosY; glfwGetCursorPos(this->getWindow(), &curPosX, &curPosY); return glm::u32vec2(curPosX, curPosY); },
		[this](const glm::i32vec2& pos) {glfwSetCursorPos(this->getWindow(), pos.x, pos.y); },
		[this](float f) {return this->sof(f); });
}

You can observe from the code, that using lambda constructs, we have provided two functions, that do getting or setting the mouse cursor position using GLFW framework. The reason of choosing this implementation again is, that I did not want to mix camera's class with some concrete framework. This way, you can practically just use this camera (or SimpleWalkingCamera as well) in your projects and all you have to do is to provide your specific implementations of those functions to make it work!

The scene itself has not changed from the previous tutorial, but as you can see in the picture below, we can look at it from bird's perspective now :

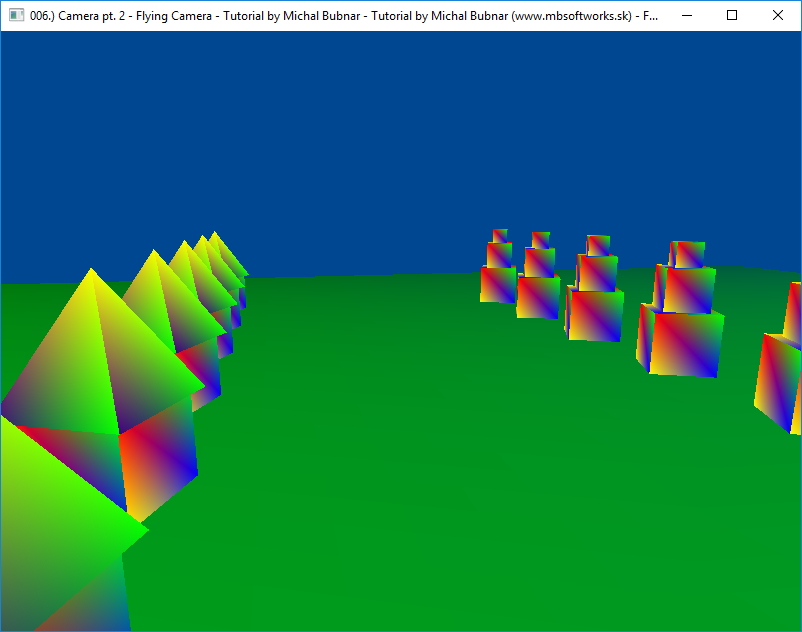
This article has been not much about OpenGL itself, because the principles of this camera can be used basically anywhere. There was some more difficult 3D math involved as well, but in the end, we can move freely around the world, not restricted to the ground!

I'm planning to create a new article series dedicated to 2D and 3D math, because I feel like this might help a lot. All those concepts like cross product, dot product, normalization etc. - these require a lot more explanation than just to fit / hide it inside this article. Once it's done, I will update this paragraph and like those articles here .