Hello friends and welcome to my 11th OpenGL4 tutorial! I think we've gone a long way through so far and we are now able to achieve pretty much stuff in OpenGL. This tutorial unravels another option of rendering things in OpenGL and it's Indexed Rendering. A good object to be rendered using indexed rendering is torus. So let's get into it!

So far, we've been rendering things by preparing one VBO and filled it with data. This was fine until now. But many times in rendering, there are objects, that tend to have repetitive vertices - like multiple triangles share those vertices. In this case, it's really not nice to copy and paste the same vertex everytime, because if you would want to change it, you would have to change it everywhere (copy pasting in programming is generally bad idea). So what is indexed rendering about? It's pretty simple - first, we create an array of vertices. As usual, vertices in array have indices. Let's make an example:

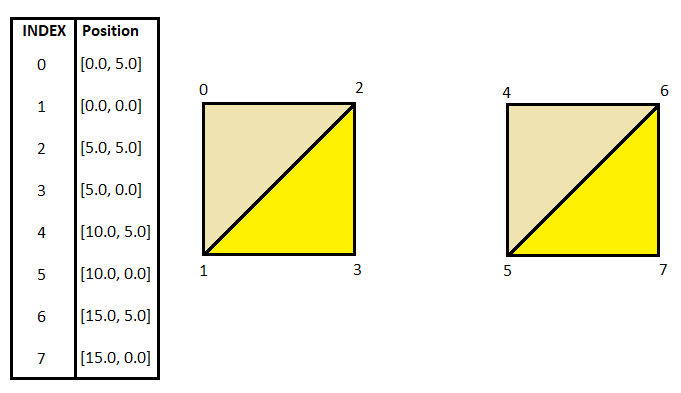
This example is really simplified - we can see a table with eight 2D vertices. My intentions with those vertices are to render two quads as you can see depicted in the picture using triangle strip. To be more exact, I have to make two separate triangle strip calls. One call would include rendering vertices [0,1,2,3] and second call would include vertices [4,5,6,7]. This way, we would achieve exactly our goal . So the whole point of indexed rendering is this - we have to prepare a list of vertices beforehand and then address vertices using indices.

Indexed rendering seems pretty easy right? Yeah, I must admit, it's nothing super difficult to understand, but what's the problem with rendering those two quads above? We would have to issue two rendering calls to render two quads. That's not that much, but if we have to render let's say 1'000'000 quads in the scene, do we really have to issue 1'000'000 drawing calls? Of course not! There is a better way! What you can see here is, that we are basically making two separate triangle strip calls - one with [0,1,2,3] and one with [4,5,6,7]. In another words, we have restarted rendering once.

Can we somehow incorporate this restarting into rendering call? Of course we can! OpenGL allows us to define so-called Primitive Restart Index. This index does not define any vertex, but instead tells OpenGL it should restart the rendering. In our case, we are already using indices 0 to 7, so a good candidate for primitive restart might be index 8. So if we set everything correctly, then we can render those two quads above using just one rendering call by defining indices [0,1,2,3,8,4,5,6,7]! By the way, you can choose arbitrary number beyond number of vertices for primitive restart, even 7901 in this case, but you have to tell OpenGL which number means primitive restart. I usually just take the number of vertices - in our case, we have 8 vertices, so primitive restart index is 8 .

There is one interesting aspect to discuss here. We cannot define different indices for different vertex attributes. We can have only one array of indices for all vertex attributes! This fact makes some objects, like cube not suitable to render with indexed rendering. Cube has 8 vertices only, but they have different texture coordinates and normals on different sides. Using indices here will actually consume more memory (because we would have to define multiple combinations of the same position and different vertex coordinate and normal) than not using them .

And now, it's finally time to implement torus with indexed rendering!

For those of you, who don't know what torus is, it's that ring (or donut ) shaped object, which can be defined easily parametrically and it looks like this:

The object is probably well known to you and you've seen it. How to define its surface then? What we need is actually just two angles to parametrize the torus - main radius, which is the distance from the center of the torus to the center of the tube and tube radius, which is radius of the tube, respectively. The equation looks like this (taken from Wikipedia):

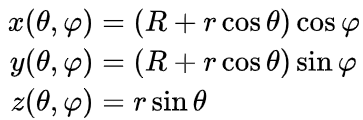
To explain this - if you take those two angles - φ (Phi) and θ (Theta) and insert them into the equations, you get [x, y, z] coordinates of the point on the torus! φ is the angle, with which we go around the whole torus (main angle) and θ is the angle, which we orbit the tube around with (tube angle) .

If you want to get the whole surface (all the points) of the torus, you would have to enter all possible combinations of φ and θ. Because angles are real numbers, you would get ∞*∞ = 2*∞! That means two times infinity ! Just kidding - of course we can't get all the points and we don't need to. What we can do however is to agree upon, how many times will we subdivide the torus around and then within the tube. We will define two additional variables - main segments - how many times we subdivide around the torus and tube segments - how many times we subdivide one part of the tube itself. To demonstrate this, this is an example of 20 major segments (and 20 tube segments, but it's not that much visible here):

Each "tick" generates one segment of the torus. What you can see here is, that the ending points of one segment are actually same as the beginning point of another segment! That's why indexed element here makes perfect sense. So when we render the torus, we can render every main segment separately with triangle strips and then use primitive restart index to start another segment. And when we have the amount of required segments, we can then write two for loops to go through all major segments (and use Theta angle and increase it by the correct amount) and another nested for loop to go through all tube segments (and use Phi angle and increase it by correct amount) .

First of all, let's create a new 3D static mesh class, that supports indexed rendering:

#pragma once

#include "staticMesh3D.h"

namespace static_meshes_3D {

class StaticMeshIndexed3D : public StaticMesh3D
{
public:
	StaticMeshIndexed3D(bool withPositions, bool withTextureCoordinates, bool withNormals);
	virtual ~StaticMeshIndexed3D();

protected:
	VertexBufferObject _indicesVBO;
};

};

As you can see, we inherit this class from the base StaticMesh3D class and we extend it with one new private member _indicesVBO. As you already might guess, this VBO will hold indices that we use to render our mesh. That's really it and there is not much more I can say about this class.

Now that we have this, we can proceed with creating Torus class:

class Torus : public StaticMeshIndexed3D
{
public:
	Torus(int mainSegments, int tubeSegments, float mainRadius, float tubeRadius,
		bool withPositions = true, bool withTextureCoordinates = true, bool withNormals = true);

	void render() const override;
	void renderSpecial(int segments) const;

	float getMainRadius() const;
	float getTubeRadius() const;

private:
	int _mainSegments;
	int _tubeSegments;
	float _mainRadius;
	float _tubeRadius;

	int _numIndices = 0;
	int _primitiveRestartIndex = 0;

	void initializeData() override;
};

Its members should be pretty self explanatory by now - you can see, that we hold the number of main segments and tube segments alongside with their radii. Then we keep the count of the indices for indexed rendering and primitive restart index . What is really important here is the way we generate the vertices and indices. So let's go through the initializeData() function step by step:

void Torus::initializeData()
{
	if (_isInitialized) {
		return;
	}

	// Calculate and cache counts of vertices and indices
	const auto numVertices = (_mainSegments+1)*(_tubeSegments+1);
	_primitiveRestartIndex = numVertices;
	_numIndices = (_mainSegments * 2 * (_tubeSegments + 1)) + _mainSegments - 1;

	// Generate VAO and VBOs for vertex attributes and indices
	glGenVertexArrays(1, &_vao);
	glBindVertexArray(_vao);
	_vbo.createVBO(getVertexByteSize() * numVertices);
	_indicesVBO.createVBO(sizeof(GLuint)*_numIndices);

    // ...
}

First of all, we have to prepare many things. We need to calculate number of vertices we will generate. How much is that? Well we have _mainSegments around the torus and _tubeSegments around the tube. So the first guess might be _mainSegments*_tubeSegments. It's almost correct! There is one thing we have to account for - we have to duplicate the start and end of one roundabout - although the vertex positions and vertex normals are same, the texture coordinates are different. At the beginning, texture coordinate is 0.0 somewhere and at the end it can't be 0.0 again, but rather 1.0 (or how many times we want to map the texture). So the correct amount of vertices is (_mainSegments+1)*(_tubeSegments+1) . Number of rendering indices is explained a bit further.

(an opportunity for small optimization here and a good exercise for you maybe - if we had no texture coordinates, we don't have to duplicate starting and ending vertices of main and tube segments, so we could reduce amount of generated vertices - think about it ).

As mentioned before, we have to restart primitive after rendering every main segment - that's why we have to calculate primitive restart index. Because we already have number of vertices, we can use this number as primitive restart index! I have already shown before, that if I have 8 vertices with indices 0 through 7, their count - 8 - is pretty good candidate for primitive restart index .

Having this, we prepare VAO and both VBOs - one for vertices and one for indices and we allocate enough space for them to hold all the data (so that setting it up is faster and std::vector, that is internally used does not have to re-allocate).

Let's have a look at the code, that generates position of vertices:

void Torus::initializeData()
{
	// ...

	auto mainSegmentAngleStep = glm::radians(360.0f / float(_mainSegments));
	auto tubeSegmentAngleStep = glm::radians(360.0f / float(_tubeSegments));

	if (hasPositions())
	{
		auto currentMainSegmentAngle = 0.0f;
		for (auto i = 0; i <= _mainSegments; i++)
		{
			// Calculate sine and cosine of main segment angle
			auto sinMainSegment = sin(currentMainSegmentAngle);
			auto cosMainSegment = cos(currentMainSegmentAngle);
			auto currentTubeSegmentAngle = 0.0f;
			for (auto j = 0; j <= _tubeSegments; j++)
			{
				// Calculate sine and cosine of tube segment angle
				auto sinTubeSegment = sin(currentTubeSegmentAngle);
				auto cosTubeSegment = cos(currentTubeSegmentAngle);

				// Calculate vertex position on the surface of torus
				auto surfacePosition = glm::vec3(
					(_mainRadius + _tubeRadius * cosTubeSegment)*cosMainSegment,
					(_mainRadius + _tubeRadius * cosTubeSegment)*sinMainSegment,
					_tubeRadius*sinTubeSegment);
				
				_vbo.addData(&surfacePosition, sizeof(glm::vec3));

				// Update current tube angle
				currentTubeSegmentAngle += tubeSegmentAngleStep;
			}

			// Update main segment angle
			currentMainSegmentAngle += mainSegmentAngleStep;
		}
	}

	// ...
}

What we're doing here is that we are going through every main segment and with it through every tube segment. With main segment angle I refer to angle φ (Phi) and with tube segment angle I refer to θ (Theta) that you see in the equation. Then we just do the calculation of vertex by putting all the variables (angles with their sines / cosines) and we get position on the surface of the torus! And that is what finally gets into the VBO. At the end of the loops, we are just updating the angles by precalculated step

Following code generates texture coordinates of the torus:

void Torus::initializeData()
{
	// ...

	if (hasTextureCoordinates())
	{
		auto mainSegmentTextureStep = 2.0f  / float(_mainSegments);
		auto tubeSegmentTextureStep = 1.0f / float(_tubeSegments);

		auto currentMainSegmentTexCoordV = 0.0f;
		for (auto i = 0; i <= _mainSegments; i++)
		{
			auto currentTubeSegmentTexCoordU = 0.0f;
			for (auto j = 0; j <= _tubeSegments; j++)
			{
				auto textureCoordinate = glm::vec2(currentTubeSegmentTexCoordU, currentMainSegmentTexCoordV);
				_vbo.addData(&textureCoordinate, sizeof(glm::vec2));

				currentTubeSegmentTexCoordU += tubeSegmentTextureStep;
			}

			// Update texture coordinate of main segment
			currentMainSegmentTexCoordV += mainSegmentTextureStep;
		}
	}

    // ...
}

This one here is a bit simpler. We are doing same thing as before - looping through all the main segments and within them through all tube segments. But this time, we are just increasing the texture coordinates linearly with increasing segments and this is added to the VBO. I have decided to map the texture once around the tube and twice around the whole torus. The result is nice and I am happy with it, albeit I have seen some other equations (like this one at SIGGRAPH webpage), but I was too lazy to try it out . So maybe it's worth a try, but for now I am satisfied with this simple way anyway .

We haven't discussed normals yet, but they are really important and used in lighting equations (we will get to that in later tutorials). Following code calculates normal vectors - it's just combination of sines and cosines of φ (Phi) and θ (Theta) angles:

void Torus::initializeData()
{
	// ...

	if (hasNormals())
	{
		auto currentMainSegmentAngle = 0.0f;
		for (auto i = 0; i <= _mainSegments; i++)
		{
			// Calculate sine and cosine of main segment angle
			auto sinMainSegment = sin(currentMainSegmentAngle);
			auto cosMainSegment = cos(currentMainSegmentAngle);
			auto currentTubeSegmentAngle = 0.0f;
			for (auto j = 0; j <= _tubeSegments; j++)
			{
				// Calculate sine and cosine of tube segment angle
				auto sinTubeSegment = sin(currentTubeSegmentAngle);
				auto cosTubeSegment = cos(currentTubeSegmentAngle);

				auto normal = glm::vec3(
					cosMainSegment*cosTubeSegment,
					sinMainSegment*cosTubeSegment,
					sinTubeSegment
				);
				_vbo.addData(&normal, sizeof(glm::vec3));

				// Update current tube angle
				currentTubeSegmentAngle += tubeSegmentAngleStep;
			}

			// Update main segment angle
			currentMainSegmentAngle += mainSegmentAngleStep;
		}
	}

    // ...
}

Now that we have all vertex attributes in the VBO, all we have to do is to fill VBO containing indices with data. Below you can see the code, that is generating those indices:

void Torus::initializeData()
{
	// ...

	GLuint currentVertexOffset = 0;
	for (auto i = 0; i < _mainSegments; i++)
	{
		for (auto j = 0; j <= _tubeSegments; j++)
		{
			GLuint vertexIndexA = currentVertexOffset;
			_indicesVBO.addData(&vertexIndexA, sizeof(GLuint));
			GLuint vertexIndexB = currentVertexOffset + _tubeSegments + 1;
			_indicesVBO.addData(&vertexIndexB, sizeof(GLuint));
			currentVertexOffset++;
		}

		// Don't restart primitive, if it's last segment, rendering ends here anyway
		if (i != _mainSegments - 1) {
			_indicesVBO.addData(&_primitiveRestartIndex, sizeof(GLuint));
		}
	}

	_vbo.bindVBO();
	_vbo.uploadDataToGPU(GL_STATIC_DRAW);
	setVertexAttributesPointers(numVertices);

	_indicesVBO.bindVBO(GL_ELEMENT_ARRAY_BUFFER);
	_indicesVBO.uploadDataToGPU(GL_STATIC_DRAW);

	_isInitialized = true;
}

Because the torus is rendered using triangle strip and every torus main segment represents one triangle strip rendering batch, we need to take one vertex from the current segment and another vertex from the next main segment. That is why GLuint vertexIndexA = currentVertexOffset and GLuint vertexIndexB = currentVertexOffset + _tubeSegments + 1 - we have taken current vertex and vertex on the same level in the tube circle from the next segment. You might ask why is there plus 1 in vertexIndexB - it's because we have duplicated the first and last point because of that problem with texture coordinates not being same . Those two indices are then added to the indices VBO.

At the end of each main segments for loop, we must add primitive restart index. We do this in all but last repeat. Why is it so? Well, restarting primitive at the last main segment is not necessary, because we are not going to render anything else after. If we add it there, it won't change anything - we would have restarted primitive and then ended drawing. But this way we just end drawing and there is no restart needed! The total number of indices used to render torus is calculated as follows:

_numIndices = (_mainSegments * 2 * (_tubeSegments + 1)) + _mainSegments - 1;

This piece of code requires a bit of explanation - to render every main segment, we need to have 2 * (_tubeSegments + 1) indices - one index is from the current main segment and one index is from the next segment, that is why 2 times. Plus 1 is for that extra duplicated start / end vertex at each of the tube segment. We multiply all this by the number of main segments. At the end of this equation, we still have + _mainSegments - 1. This one is the number of primitive restart indices! We restart every main segment except the last one, that is why minus 1 at the end . We will need this number for rendering.

When the indices are prepared in VBO too, we can now send the data to the GPU. First, we send vertex data and then indices data. Very important piece of code is binding indices VBO with GL_ELEMENT_ARRAY_BUFFER! With this we tell OpenGL, that this VBO contains indices for rendering, not vertex data.

Now that we have all set up, we can finally render our torus using indexed rendering. The code doing just that follows:

void Torus::render() const
{
	if (!_isInitialized) {
		return;
	}

	glBindVertexArray(_vao);

	glEnable(GL_PRIMITIVE_RESTART);
	glPrimitiveRestartIndex(_primitiveRestartIndex);
	glDrawElements(GL_TRIANGLE_STRIP, _numIndices, GL_UNSIGNED_INT, 0);
	glDisable(GL_PRIMITIVE_RESTART);
}

First of all and as usual, we bind the vertex array object. Now we have to enable primitive restart - you don't need this always, so that's why you have to enable it in order to use it. After enabling it, we must also set the desired primitive restart index. Now we can render using glDrawElements function! It takes 4 parameters - in order they are the primitive type (GL_TRIANGLE_STRIP), the the total number of indices to render, data type of one index (GL_UNSIGNED_INT) and finally starting index of rendering (we simply render whole buffer, so that's why 0). You can experiment with those numbers to render quarter of torus, half of torus etc. to get the grasp of it .

And that's about it! After so much information at once, result looks like this:

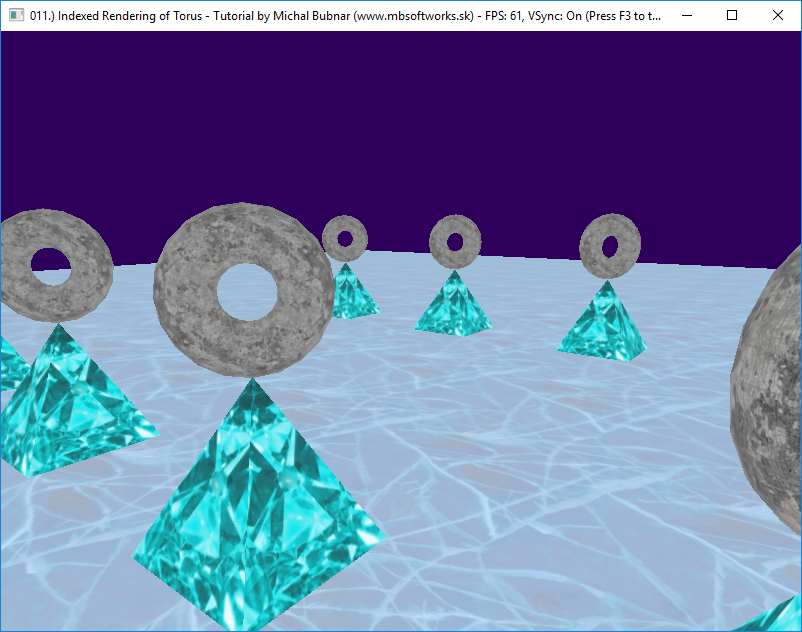
I won't lie - writing this article took me several hours, I've done it in several takes . But I hope it was worth it and you've learned a lot today . I guess you can consider implementing torus this way as advanced stuff, not your everyday OpenGL stuff. In the next article, we will discuss, how to output text over OpenGL scene using FreeType library, so stay tuned!